Algorithms

binary search - binary search on tree or array

subarray

avl trees

https://frontendmasters.com/courses/algorithms/

Big O Time Complexity

Big O is a way to categorize your algorithms time or memory requirements based on input. It is meant to generalize the growth of your algorithm or how fast does computation or memory grow?

Often it will help us make decisions about what data strucures and algorithms to use. Knowing how they will perform can greatly help create the best posible program out there.

function sum_char_codes(n: string): number {
  let sum = 0;
  for (let i = 0; i < n.length; ++i) {
    // convert the string as a sequence of UTF-16 code units
    sum += n.charCodeAt(i);
  }

  return sum;
}

How can you tell that this code is O(N) time complexity?

Simplest trick for complexity is Look for loops

Important concepts

1. growth is with respect to the input

2. Constants are dropped

O(2N) -> O(N) and this makes sense. That is because Big O is meant to describe the growth of the algorithm. The constant eventually becomes irrelevant.

Example below is also O(N)

function sum_char_codes(n: string): number {
  let sum = 0;
  for (let i = 0; i < n.length; ++i) {
    // convert the string as a sequence of UTF-16 code units
    sum += n.charCodeAt(i);
  }

  for (let i = 0; i < n.length; ++i) {
    // convert the string as a sequence of UTF-16 code units
    sum += n.charCodeAt(i);
  }

  return sum;
}

Take the following:

N = 1, O(10N) = 10, O(N^2) = 1

N = 5, O(10N) = 50, O(N^2) = 25

N = 100, O(10N) = 1000, O(N^2) = 10.000 // 10x bigger

N = 1000, O(10N) = 10000, O(N^2) = 1.000.000 // 100x bigger

N = 10.000, O(10N) = 1.000.000 , O(N^2) = 100.000.000 // 1000x bigger

Practically speaking, constants are extremely important. Theoretically they're not important, that is because we're not trying to get exact time, but it's how does it grow?

There is practical vs theoretical differences

Just because N is faster then N^2, doesn't mean practically its always faster for smaller input.

Therefore O(100N) is faster then O(N^2) but practically speaking, you would probably win for some small set of input.

But just like in sorting algorithms, often it will use insertion sort for smaller subsets of data. Because insertion sort, though slower in theoretical terms, because it is O(N^2) is actually faster then say quicksort witch is log(N) when it comes to small datasets

Worst Case

In BigO we often consider the worst case. Especially in interviews.

Therefore any string with E in it will terminate early (unless E is the last item in the list). ITS STILL 0(N)

function sum_char_codes(n: string): number {
  let sum = 0;
  for (let i = 0; i < n.length; ++i) {
    const charCode = n.charCodeAt(i);
    // Capital E
    if (charCode === 69) {
      return sum;
    }
    sum += charCode;
  }
  return sum;
}

Important concepts

1. Growth is with respect to the input

2. Constants are dropped

3. Worst case is usually the way we measure

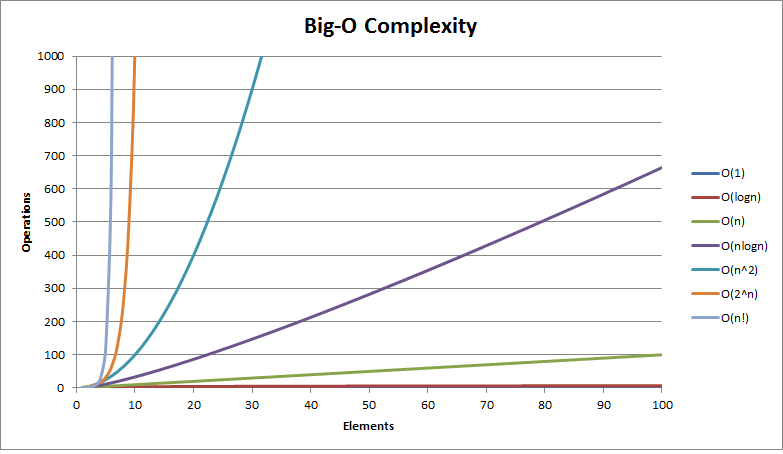
O(N^2)

function sum_char_codes(n: string): number {
  let sum = 0;
  for (let i = 0; i < n.length; ++i) {
    for (let j = 0; j < n.length; ++j) {
      sum += charCode;
    }
  }
  return sum;
}

O(N^3)

function sum_char_codes(n: string): number {
  let sum = 0;
  for (let i = 0; i < n.length; ++i) {
    for (let j = 0; j < n.length; ++j) {
      for (let k = 0; k < n.length; ++k) {
        sum += charCode;
      }
    }
  }
  return sum;
}

O(n log n)

Quicksort

O(log n)

Binary search trees

There is technically a bunch of different ways to measure the complexity of algorithms like Stata, little omega, but in general the easiest one to use is the "Upper Bound".

Arrays Data Structure

Array is unbreaking memory space in which conains a certain amount of bytes.

How memory is interpreted is based on what you tell the compiler how to interpret it.

Because an array is simply a collection of bits, we'll instruct the compiler on how to interpret that memory.

This means we'll take one bunch of bits from the array and treat them like a single number. This means we'll notify the compiler that that particular group of bytes in memory has a special meaning.

Just because it's contiguous, just because is's all one piece of memory doesn't mean that it has any specific meaning until you give it meaning. So, an array is effectively just a big, long version of group of bites.

If we have A=int[3] that meains i want three ints in contiguous space, unbreakable like for me to be able to use.

If you wanted A0, it is really telling the compiler go to memory address of A, then add in the offset of zero multiplied by how big my type is, because if your time is 32 bits or 4 bytes, index one has to be 4 bytes into the array or memory space. And that's kind of what creates an actual array.

When you want to insert something in array, it doesn't insert it, it actually overwrites it. It do not get to grow your array into more memory, because what happend if right after that array is stored value for user name. If you grow array, it will overide user name. So we can't just grow array just simply. If you want to delete value from array, you don't delete something out of contiguous memory, it will set it to zero.

What is BigO for array?

If you want to insert something into array, it will do with this formula:

a + width * offset

a is memory address

width of type which is usualy specified in bytes like, 32 bit integer is 4 bytes

offset is position for that place in array - a[2] - offset is 2

BigO for array is O(1) - constant time, because nothing in this formula goes over the entire array. We do not have to walk to that position, we know width of type and the offset, we multiply them together, get to that position and read out the value.

It doesn't mean we literally only do one thing. It just means we do constant amount of things no matter what the input is, it does not grow with input at all.

Example on how to count on Big(o)

Assume we have a sorted array and want to find our value.

We don't have to start searching from the beginning. We can skip right to 10% of N and see if that number equals my value. If we don't find value, we'll jump another 10% and see if that value is equivalent to my value and again it is not equals, but it is higher than my value. Then we'll go back 10% and run a linear search between 10% and 20%.

Worst case scenario is that we just keep jumping by 10% until we reach the end of the array, which means we have some of the very last portion of the array unsearched, and we will then execute a linear search for that last 10% of the array.

Big O for this example is O(10 + 0.1N) but when we ignore constants then our running time is O(N)

Practically, this example is 10 times better than a linear search, but theoretically, if we have a million-element array. This algorithm will be significantly slower. The algorithm becomes significantly slower as the number of elements increases.

If N was 10 000 and now it is milion, Algorithm is 100 times slower, but it is still 10 times faster then linear search.

And that is problematic. We didn't improve the algorithm. We just improved it practically speaking.